Y=ax2乗のグラフ書き方 まとめ お疲れ様でした! 放物線のグラフを書くためには 丁寧に点を取って、それらをなめらかーに結ぶ! これだけですね。 何度も練習すれば 誰にでも簡単に書けるようになります。 レッツ! 練習 (/・ω・)/合成関数の微分公式と例題7問 レベル ★ 基礎 極限,微分 更新日時 合成関数の微分は(かたまりで微分)×(かたまりの微分) 合成関数を微分する方法を2通り紹介します。 また,合成関数の微分について7つの例題を解説します。 目次 合成Try IT(トライイット)のカッコ×カッコの公式2 (x+a)^2,(x-a)^2の練習の映像授業ページです。Try IT(トライイット)は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る(トライイットする)ことにより「わからない」をなくすことが出来ます。
指数方程式
Y=x2乗-3 グラフ
Y=x2乗-3 グラフ-1 y = − x2 2 C (6) y = x2 4 1!2 (7) y = Cx1 (8) y2 = C(2x− 1) (9) y =2x (10) y = e−cosx 例題12-2 dy dx = y xを解きなさい (例題12-2の解答) dy dx = yの解y = Cexp(x)を用いて,y = C(x)exp(x) とおいて, C(x)に関する微分方程式をつくる下記文献では、「0,∞) で定義された1変数関数 y=f (x)= x 3 」による「非負の実数y」の逆像を立方根と呼ぶ。 ・小平『解析入門I』§23a) (p);n乗根一般。 ・ 松坂『解析入門1』32E例(p113);n乗根一般。 ・赤攝也『実数論講義』§65定義653(p197)




例題で学ぶ高校数学 Y Ax2 Q
つまり, を2乗すると3になりますね。 では, を2乗してみると,どうなるでしょうか? ここで,①,②より, と言えます。 この両辺の( )の中を比較して, となります。 一般に, と定義します。 例えば, , です。 さらに,指数が, ではなく, の場合はどうなるかを考えましょう。 は,本当は, の2を省略して書いたものなのです。 つまり,3の 乗が と(2)の場合も2乗の式は x 2 −2pxp 2 となって最後の項が p 2 になっていることに注意すると,逆の計算をするときは −p 2 としなければならない. (2)→ x 2 − 2p x p 2 =(x− p ) 2X 2 2次関数の最も簡単な関数は y =x2 y = x 2 である.この関数についてグラフを考える. x x の値3,2,1,0,1,2,3に対する y y の値をを下の表に示す. 各 x x , y y の組に対応する点を座標平面に描くと左下の図のようになる.表のような y = x2 y = x 2 の
1/2乗がルートと等しくなる理由 さてそれでは、本題の解説に入りましょう。 今はまだ がどういうものか分かっていません。 しかし、 が であることは分かるはずです。 なぜならばすでに、 「 の 乗の 乗とは、 の 乗に等しくなる」 という事が定め x2乗と聞いて、こんな放物線を思い浮かべたり、 微分 と聞いて、こんなイメージが浮かぶ人は、かなり数学を勉強したのだろうと思う。 でも、ここではいったん放物線のことは忘れて、 x2乗とは、以下のように一辺xの正方形を順番に並べたものだと考えてみよう。 ここで、とある正方形と、すぐ隣の正方形との差分は、こんな風になる。 うんと近くの隣同士だっ x2乗+ (y 3√x2乗)2乗=1 とありますが,3は係数ではなく 正しい式は x² (y∛x²)²=1 ① で,♡を描きたいのでしょう. ①は陰関数ですが, dy/dx=0 という方程式の実数解を正確に求めることができなければ,増減の様子が分からず,微分法を用いてグラフを
もう少し簡単な式から考えてみましょう。 (x1)2乗 = x2乗2x1 はわかりますよね? (xa)2乗 = x2乗2axa2乗 も大丈夫かな? 下の式で、右辺のa2乗を左辺に移動しましょう。 どうなりますか? これと今回の問題を比べて見てください。 こういう変形に慣れると、問題を解く力がワンランク上がります。「2乗に比例する関数 (y=ax²) で、 "変化の割合"は、 "a の値"とは違うもの なのですか?」 すごく良い質問ですね! 結論から言うと、その通りです。 「2乗に比例する関数」 では、 "変化の割合"と"a の値"は 違うものになります。具体例で学ぶ数学 > 微積分 > y=xe^x^2の積分、微分など 最終更新日 ∫ x e x 2 d x = 1 2 e x 2 C ( x e x 2) ′ = ( 1 2 x 2) e x 2 目次 不定積分



Yx2乗 ニスヌーピー 壁紙



因数分解とグラフ 中学から数学だいすき
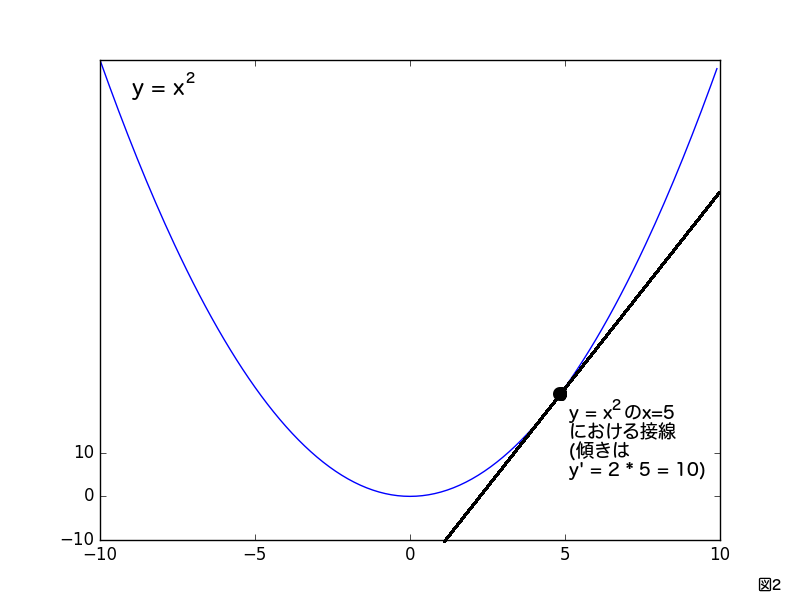
(類題12-1の解答) (1) y = −log(C −ex) (2) y = Ce12x 2 (3) x2 y2 = C (4) y = log(ex C) (5) y =0;2/5 円 x 2 +y 2 +lx+my+n=0(5分38秒) 3/5 平方(かっこの2乗)の形の作り方(5分17秒) 4/5 方程式から円の中心の座標と半径を求める方法(4分42例題 (1) y = x 2 上の点 (1, 1) における接線の方程式 y'= 2x だから x = 1 のとき y'= 2 y−1 = 2(x−1) y = 2x−1 ・・・答 y = x 2 上の点 (1, 1) における法線の方程式 法線の傾きは m'=− y−1 =− (x−1) y =− x ・・・答 (2) y = x 2 −2x における傾き −4 の接線の方程式




直線y 2x 2が 円x2乗 Y2乗 8に切り取られてできるゲームの長さを求めよ これ分かりませんでした Peing 質問箱



2乗に比例するグラフ 中学から数学だいすき
y=ax2乗のグラフで覚えておきたい用語 まず、グラフの形は 放物線 となります。 この放物線は左右対称の形となっており、その折れ目となる線のことを 軸 といいます。関数 y=2x² について、 xの変域が次のとき、 yの変域を求めなさい 。さっそく解いていきましょう。 まずは、 "y=2x²" の対応表を作ります 。 3つの問題を見ると、 x が一番小さいときは「-4」、 一番大きいときは「4」と分かるので、 対応表は、 の 標準正規分布に従う確率変数の 2 乗和はカイ二乗分布に従う カイ二乗分布 標準正規分布 \( \mathcal{N}(0, 1) \) から n 個の標本 X 1, X 2, , X n を独立に抽出したとする。 このとき、n 個の標本の 2 乗和 Z が従う分布を、自由度 n のカイ二乗分布という。




2次関数のグラフと直線



2次関数の問題で Y X2乗 X 1のグラフがこうなるのは何故ですか Yahoo 知恵袋
0 2 エクセルで2乗の計算をするとき、どのように計算していますか。 「=2*2」というように単純に入力しているという人が多いかもしれません。 数式を知っていればより簡単に2乗の計算ができます。 今回は2乗や3乗といった指数の計算である累乗を簡潔に行う方法を紹介します。 ※本文に記載した設定方法はすべてOffice16の操作です。X 2 6x1 = 0 ←定数項を右辺に移項する x 2 6x = 1 ←左辺でxの2乗の式を作るため両辺に9を足す x 2 6x 9 = 1 9 ←左辺を因数分解すると(x3) 2 になる (x3) 2 = 10 ←平方根 x3 = ± 10 ←3を移項2乗のものを2乗のもので引いた式は、和と差の積に変換できるのが因数分解の公式3です。 4 x 2 y36 y 共通因数(4 y



1
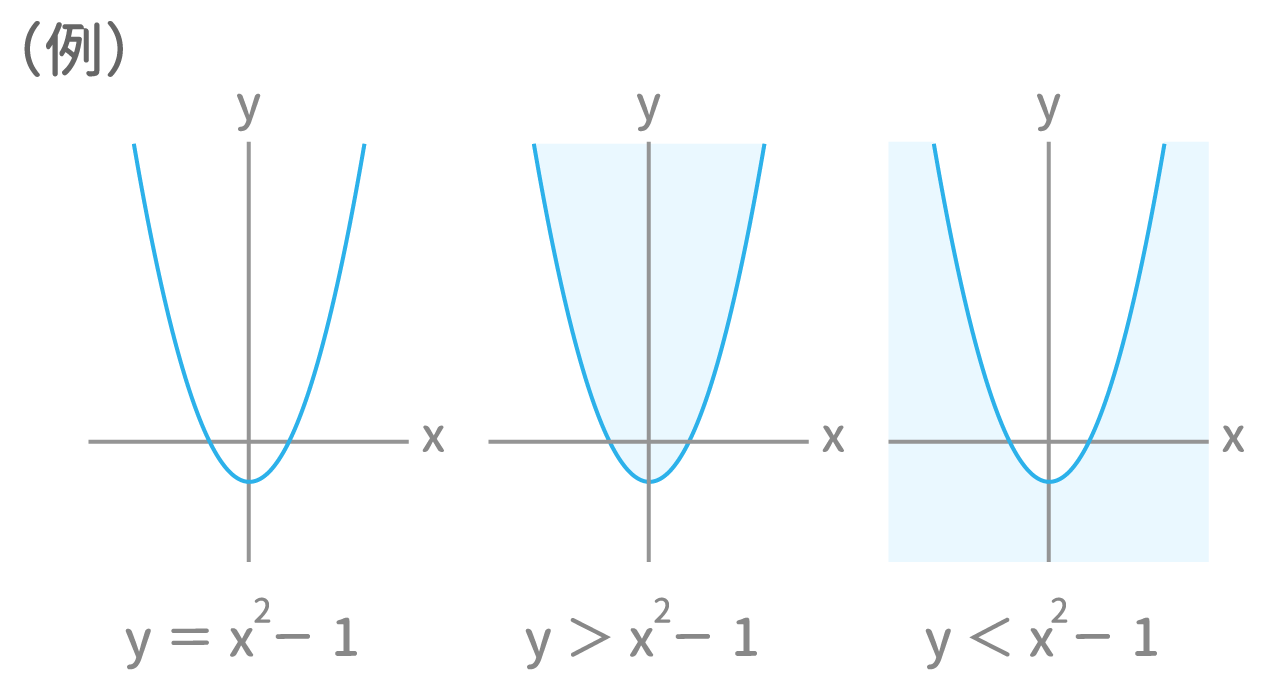



Spi 不等式と領域 最速解法 例題 Study Pro Spi
y=x 24x10を平方完成すると、 y=(x2) 2 6 ですね。 よって、この二次関数の頂点の座標は(2,6)です。 ※二次関数の頂点について深く学習したい人は、 二次関数の頂点について詳しく解説した記事 をご覧ください。例:y=x, y=x, y={2^x} グラフの縮小率を大きくすると、広い範囲が見られます。逆に、縮小率を小さくすると、原点付近を拡大できます。 指数関数について y=x 2 ではなくて、y=2 x としてみます。 指数関数と対数関数は対の関係です。X2y′ = (x − 1)y の一般解を求めよ 解答 この方程式は形式的に dy y = „ 1 x − 1 x2 « dx と書けるので変数分離形である 従って両辺を積分して より また も解なので も含めて最終的な答えは は任意の定数 I 常微分方程式– p6/31



二次関数のグラフ




Tarc8 Y X2 X 24 Descubre Como Resolverlo En Qanda
展開すると時間かかってテストの問題終わらないからだそうです。 だから、y= (2x^6/3) (3x^2/2)を微分するのも y´=dy/dx= (2/3)×6x^5 (3/2)×2xでいいそうです。 普通なら全部掛け算ちゃんとするんですがね そこで思ったんですが、 y= (1/2) (x^23x)は y基本的な関数の微分 1 x 2 問題 次の関数の導関数を微分の公式および導関数の定義式を用いて求めよ. f (x) = 1 x 2 答 f ′ (x) = − 2 x 3 解説 f (x) = 1 x 2 = x − 2 と表すことができる. 公式を用いた計算 微分の公式を用いると, f ′ (x) = − 2 x − 2 − 1 = −陰関数の微分法 y=2x1 のように y について解かれた形になっているものを陽関数, x 2 y 2 =1 のように x , y の関係式で示され, y について解かれた形になっていないものを陰関数という. 陰関数で表わされているものを微分するには,右の例のように両辺をそのまま微分すればよい.
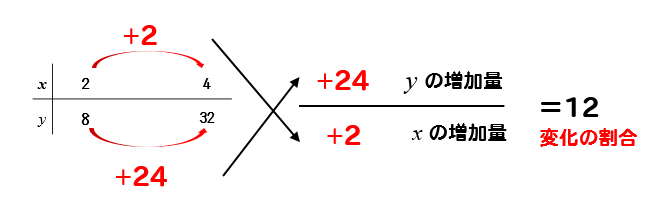



変化の割合 二次関数y Ax2の裏ワザ公式 どうやって解くの 数スタ




偏微分の意味とやり方
Y=2x 2 上の任意の点を (x,y) ,平行移動を行なった後の点を (X,Y) とします。すると, X=x2,Y=y1 となります。よって,古い座標を新しい座標で表すと, x=X2,y=Y1 となり,この関係式を y=2x 2 へ代入すると, Y1=2(X2) 2 発展問題もアリ! |中学数学・理科の学習まとめサイト! y=ax2乗aの求め方についてパターン別に解説! 発展問題もアリ! を求めろって言われても 何をすればいいの! ? というわけで、今回の記事では中3で学習する関数 の単元から「 の求め積分値の計算 極座標を用いて ガウス積分を求める標準的な方法として、以下のアイデアはポアソンまで遡れる : 平面 R 2 上の函数 exp{−(x 2 y 2)} = exp(−r 2) を考え、これを2通りの方法で計算する。 一つは直交座標系に関する二重積分として計算し、その値は求める値の平方になることを



3分の2乗の説明




二次関数の変域を求める問題の解き方の3つのコツ Qikeru 学びを楽しくわかりやすく
グラフ y=1/2x^2 y = 1 2 x2 y = 1 2 x 2 1 2 1 2 と x2 x 2 を組み合わせます。 y = x2 2 y = x 2 2 与えられた放物線の性質を求めましょう。 タップしてもっと手順を表示する Rewrite the equation in vertex form タップしてもっと手順を表示する x 2 2 x 2 2 を平方完成します。 因数分解の問題の解き方とコツ。 2乗・3乗公式とたすきがけ Tooda Yuuto 17年11月8日 / 18年2月21日 数の中には「2つ以上の数のかけ算」に変形できるものがたくさんあります。 例えば x 2 − 1 は ( x 1) ( x − 1) というかけ算に変形できますよね。 このように 特定の数を「2つ以上の数のかけ算」に変形する ことを、 因数分解 と言います。 因数分解の中でも 21 = 3 × 7Y = ax 2 に xとyの値を代入して比例定数を求める ことができる。 1次関数とちがい、1点を代入するだけで式が出る。 yがxの2乗に比例し、x=2のときy=でした。



図のように関数y X2乗とy Ax Bのグラフが 2点a Bで交わ Yahoo 知恵袋
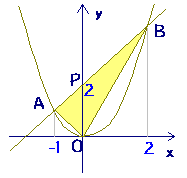



2次関数のグラフと直線
y=2(x3)2乗のグラフはy=①x2乗のグラフをx軸方向に②だけ平行移動したもので、その放物線の軸は直線x=③ 頂点の座標は(④⑤)である。 語群 3,2,3,2,0,1,1,4 上の問題を解いてください! 全くわかりません>_< 答えは語群の中から選びます。グラフ ・R=(-∞,∞) で定義された1変数関数y=f (x)=x 2 のグラフは、 ・原点(0,0)でx軸に接する ・下に凸な ・R 2 上の放物線 である。ワードで2乗を入力する場合、「2」を選択して「右クリック⇒フォント⇒文字飾りの上付き」にチェックを入れましょう。 またワードの「ホーム⇒フォント」にxの2乗を意味するボタンがあります。 2を選択して、このボタンをクリックすれば2乗に変換されます。 今回はワードで2乗を入力する方法、上付き文字の表し方、数式の使い方について説明します。 2乗の



指数方程式




微分係数の問題なんですけど Y X2乗 1の X 2ってどういうことですか Clear




例題で学ぶ高校数学 Y Ax2 Q




4乗のグラフ 2乗のグラフは学校で習いました 4乗のグラフはどんな 数学 教えて Goo




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ



Mathematics 関数と証明 大阪府公立 22年前期理数科 働きアリ




Y 1 X 2乗 のグラフってどんなんですか 大体でいいので教えてください Clear




この問題区切りより下が間違っていて答えはy x2乗 x 6なのですがどこが間違って Clear




解説がわかりません なぜy x2乗 3xを平行移動した放物線の二次関数はy x2乗 Clear
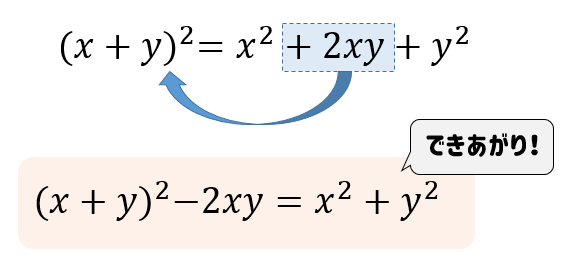



二乗足す二乗の公式 なんでこんな変形になる どんな場面で活用する 数スタ



F X X2乗 3x 2の解とグラフの答えをお願いいたします 解 って Yahoo 知恵袋
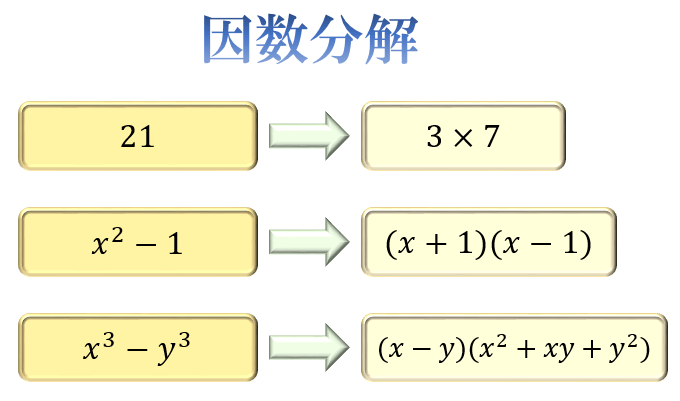



因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ




この関数のグラフを描きたいのですが 曲線の式は X 2 Y 3 Okwave



数学で 右の図のように 関数y x2乗のグラフ上にx座標が Yahoo 知恵袋



中3 2次関数




Yx2 Y X2 Descubre Como Resolverlo En Qanda




Y X 2 2x 3の平方完成について X 2 2x 3 X 1 2 4 となったので 数学 教えて Goo




Xの二乗に比例する関数 特徴 式 値 基 数学の解説と練習問題
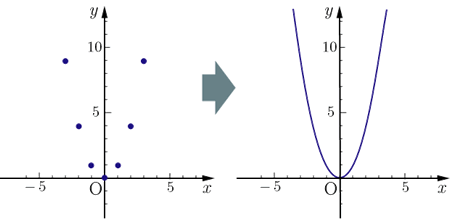



2次関数のグラフ Y X 2




基本 二次関数 Y Ax 2 のグラフ なかけんの数学ノート



Yx2乗 ニスヌーピー 壁紙
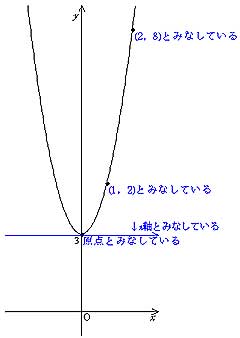



授業実践記録




y x2乗 2x 2を平方完成したらどうなりますか 途中式教えてください Clear




Aは正の定数とする 関数y X 2 4x 3 0 X A の最大値を求めよ 解き 高校 教えて Goo




3年 関数 Y X のグラフ 数学イメージ動画集 大日本図書




2次不等式の解き方 X 4x 5 0 X 4x 5 0の形をした問題 数学i By ふぇるまー マナペディア



Y X2乗 4の式で頂点と軸を求めてグラフを書けと言われました答えはわかるの Yahoo 知恵袋
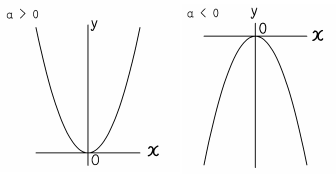



2乗に比例する関数 グラフ
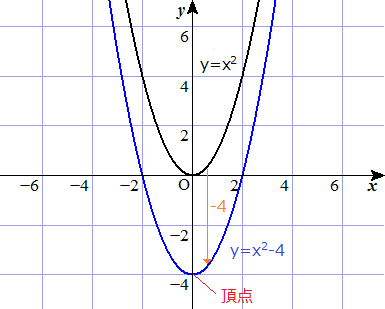



例題で学ぶ高校数学 Y Ax2 Q




数学 計算 X二乗 Xy Y二乗 X二乗 Xy Y二乗 X4乗 X二乗y二乗 数学 教えて Goo




Yx2乗 ニスヌーピー 壁紙




基本 二次関数y A X P 2のグラフ なかけんの数学ノート




関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ




中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
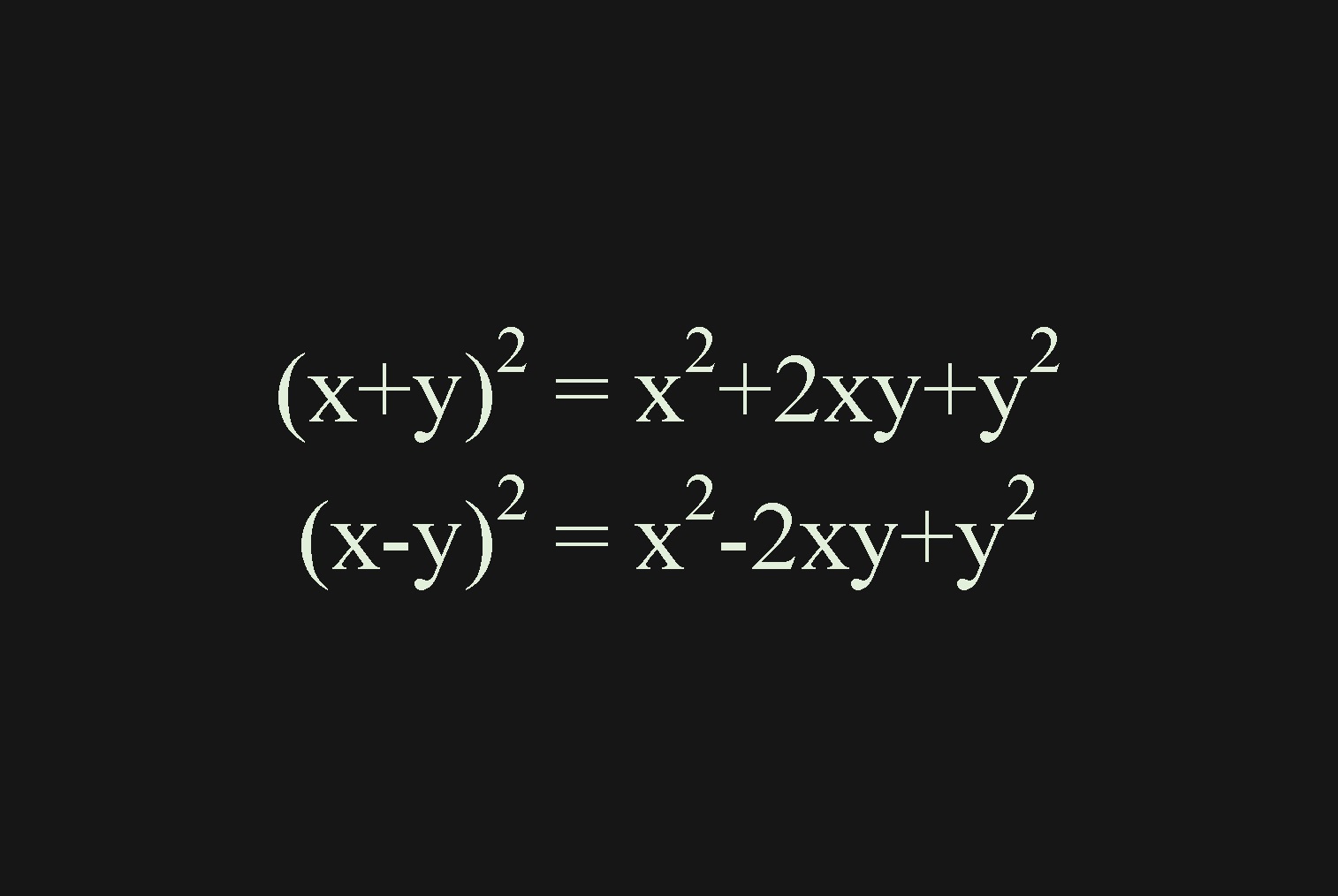



式の展開の一覧 X Y の二乗 三乗など 統計学が わかった




数学 中3 35 二次関数のグラフ Youtube



1




基本 二次関数y A X P 2のグラフ なかけんの数学ノート



高校数学 分数関数 Y X X 1 のグラフ 受験の月



二次関数のグラフ




Y x二乗 xの微分を教えてください Peing 質問箱




中学校数学 3年生 数量 2乗に比例する関数 Wikibooks




因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ




2次関数 Y A X P のグラフの書き方 グラフの平行移動 数学i By ふぇるまー マナペディア




カイ二乗分布 中学の数学からはじめる統計検定2級講座第13回 とけたろうブログ



Y 1 X2乗のグラフ Youtube




二乗足す二乗の公式 なんでこんな変形になる どんな場面で活用する 数スタ



最も人気のある Y X2乗 グラフ シモネタ



Http Www Edu City Fukuyama Hiroshima Jp Chu Johoku Revolution Actionplan Syutaiteki Manabi01 6 Shidouan K29 07m Pdf



数式のグラフ




中3数学 Y X2乗のグラフ 5分で学習 Youtube




基本 指数関数のグラフ なかけんの数学ノート




2次関数のグラフ




Y Ax2乗 変域の求め方 変域から式を作る方法について解説 中学数学 理科の学習まとめサイト




因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ



Http Www Ikushin Co Jp Shuppan Textimg 16jack Chu3hyo Sugaku Hon Pdf




2次関数 y a x p 2乗 qの形にが解けない Okwave




次の2次関数をy A X P 2乗 Qに変えてください Y X2乗 X Clear



Y x2乗 4x 4のグラフってどうなりますか 頂点と軸と凸 Yahoo 知恵袋



印刷可能 Yx2乗 シモネタ




1 2 の答えがそれぞれy X2乗 Y 4xだったのですが 解説が載っていなかっ Clear



1



2乗に比例するグラフ 中学から数学だいすき




微分係数の問題なんですけど Y X2乗 1の X 2ってどういうことですか Clear




中3数学 Y X2乗とy X2乗のグラフ 5分で学習 Youtube



2 裏業



Y Xの二乗 1 のグラフを書いてくれませんか Yahoo 知恵袋



高校数学 二次関数のx2乗の係数aの意味 学びの泉 五目スパゲティ定食 楽天ブログ



二次関数の値の変化 Y X2 4x 5を 平方完成してグラフを書く 私 Yahoo 知恵袋




中学校数学 3年生 数量 2乗に比例する関数 Wikibooks




高校数学 Y Ax 2 Bx Cのグラフ 例題編 映像授業のtry It トライイット



Q Tbn And9gcr5xwf9edrcskejqgyagxfwhnmwvaa7xrvtcx Jl9p Kp5wcn6m Usqp Cau



Y X2乗 2x 3ってどうしてこの様なグラフになるのでしょうか Yahoo 知恵袋




中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく




2次関数 変域 変域からの式の決定 基 標 数学の解説と練習問題



授業実践記録




中3数学 Y X2乗のグラフの変域 5分で学習 Youtube




Aは正の定数とする Clear



授業実践記録




Y 1 X 2乗 4 写真が分かりやすいと思います の増減 凹凸な Y 1 数学 教えて Goo




中3数学 Yはxの2乗に比例 とは 映像授業のtry It トライイット




Y x二乗 xの微分を教えてください Peing 質問箱



無料でダウンロード 関数 Yx2乗 ニスヌーピー 壁紙



Y X2乗 4の式で頂点と軸を求めてグラフを書けと言われました答えはわかるの Yahoo 知恵袋



中学数学 Y Ax 2 のグラフ 中学数学の無料オンライン学習サイトchu Su




放物線y X2乗 4ax 2b がx軸と異なる2点a Bで交わっている ただし A Clear



Y X2乗 4x 1のグラフの書き方を教えてください グラフの画像をつけ Yahoo 知恵袋



Y X 2 2x 1のグラフあってるでしょうか 解説のグラフと Yahoo 知恵袋


