図で∠ABC=∠AEDである。 A B C D E (1) 相似な三角形の組を一組答えよ。 さらにその時の相似条件を答えよ。 (2) AB=12cm, BC=8cm, AC=9cm,DがABの中点のとき つぎのそれぞれの辺の長さを求めよ。 ① AE ② DE 3番の解説 解説ページに解説がない問題で、解説をご希望の場合はリクエストを送信してください。相似比の練習問題(平行四辺形5) 問1図のように、平行四辺形ABCD の辺AD 上にAE:ED =1:2 となる点E をとり、E から 辺AB に平行な直線を引き、辺BC との交点をF とします。 三角形の相似条件 相似の問題の中でも、三角形の相似を証明する問題が多く出題されます。 ここでは、三角形の相似を証明するために必要な3つの条件を説明します。 私が実際に問題を解いた時に使う回数が多いと感じた順に書いてみました。 1つめは、 「2組の辺の比とその間の角が等しい」 という条件です。 個人的には一番使う回数が多いと感じました
相似三角形中的辅助线 学生版 教师版 沃文网wodocx Com
三角形 相似 問題
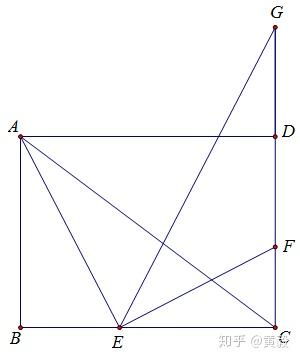
三角形 相似 問題-− 85 − 高校講座・学習メモ ベーシック数学 26 三角形の相似 問題1 2つの相似な三角形を探し、 その相似条件を示しなさい。答えは、 ずばり、 三角形 ADE A D E と三角形 CEG C E G の相似です。 一番はじめに注目した相似です。 相似比は 1 2 1 2 なので、 DE EG = 1 2 D E E G = 1 2 です。 F G F E = 1 4 F G F E = 1 4 と合わせると、下図のように長さをおけます。 より、底辺が 8x 8 x 、高



两边成比例 且夹角相等的两三角形相似 Page16 青岛版九年级数学上册电子课本 教材 教科书 好多电子课本网
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru三角形の相似条件3(2つの角) 7 友達にシェアしよう! すべての授業の「要点まとめノート」「問題・解答」をPDF無料ダウンロードできる 学校で使っている教科書にあわせて勉強できる わからないところを質問できる 会員登録をクリックまたはタップ思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げています。 図形ドリル PDFファイルをダウンロード 問題の答え合わせをTwitter上で随時受け付けております。 解けた方はお気軽に@sansu_seijin宛につぶやい
三角形の相似を使う応用問題。 解答の一行目からの流れと思考の流れのギャップを知る 自分としてはスマートに常に方針は立たないし、立たないことが大切だと思っている。 この相似を使った問題でそれを見ていこうと思う。 まずは目標の確認から→BPPQという辺の比を求めないといけない。 辺の比を求めるという情報と本文中の①、②、図形のヒントから何を補充問題 ( のところにマウスを近づけると、答えが表示されます。) 図のような三角形abcがあります。deはbcに平行に引いた直線で、三角形adeの面積は63 です。 (1) aeの長さは cmです。 (2) 三角形adeと三角形abcの面積の比は です。相似な立体の表面積・体積(1) 相似な立体の表面積・体積(2) 6 円 円周角と中心角(1) 問題一括 (2,462Kb) 解答一括 (2,734Kb) 円周角と中心角(2) 円周角と中心角(3) 等しい弧と円周角 円周角と図形の証明 円周角の定理の逆 円周角の定理の活用 7 三平方の定理
相似な三角形を使った練習問題解答 (1)∠eda ∠fda (2)上の解説参照 (3)8cm相似 練習問題 相似1 (基礎) 相似2 相似の証明1 相似の証明2 相似と線分比1 相似と線分比2 相似と線分比3 相似と線分比4 (発展) 相似5 相似6 角の二等分線と辺の比 (発展) 相似と面積比 面積比 (1) ABDと CBAにおいて ∠ABD=∠CBA (共通) ∠BDA=∠BAC=90° (仮定) よって2組の角がそれぞれ等しいので ABD∽ CBA (2) 60 13 ㎝ ABCと ADEにおいて中学3年数学練習問題 相似な三角形の比/図形と相似 中学3年数学の練習問題。 三角形の比を使って、辺の長さを求める問題の解答。 数学の基礎問題を中心に掲載。 普段の家庭学習や定期テスト・受験勉強に! 中学生 勉強なんて 怖くない ~ 勉強が苦手な中学生のために ~ TOP 中学3年 数学 練習問題



行测几何问题 相似三角形 图片欣赏中心 急不急图文 Jpjww Com




中考數學 相似三角形搞不懂這幾點 問題可就大了 每日頭條
C問題4 右図の三角形abcの辺bcを2倍、辺caを3倍、辺abを5倍にのばした点をd、e、fとして三角形defを作りました。三角形defの面積は三角形abcの面積の何倍ですか。 (デイリーサポートの解説) 3×1+5×2+4×2+1=22 (解説を区切り面積で考えたときの図)三角形 \(ABC\) と三角形 \(CDB\) は相似です。 ちなみに赤丸 \(1\) つの大きさも求まりますね。 \(36°\) です。 さて、いよいよこの問題を解く準備が整いました。 下図のように、\(DB=x(cm)\) とします。 ここで、相似な三角形に着目します。10 『相似』! なら「対応する辺」と「順番」さえ合っていればよい ① 2つの三角形が『相似』だった場合、ある辺の長さを求めるための表現は 実は自由です このあと「平行線と線分の比」や「方べき」などで 「この辺」:「この辺」は「この辺




相似三角形模型讲一线三等角问题讲义解答 豆知网



利用特殊直角三角形简化相似三角形存在性问题 知乎
相似な図形と線分比と平行の関係、その計算方法と図形をとらえる視点について応用問題を含めて学習します。 三角形と線分比 平行線と線分比 線分比と相似 線分比と相似 線分比と相似 線分比と相似 線分比と相似 線分比と相似 1)2組の角度が同じならその三角形どうしは相似になる 2)相似の三角形の辺は比例関係から求められる(事が多い) 3)直角三角形の中に正方形が入った問題は相似の三角形を作って解く 相似+三角形のテクニック3つ!練習問題4 下図において、 ABCと相似な三角形をすべて見つけ、記号を使って表し、相似条件も答えなさい。 <前: L29 相似な図形とその性質 の問題 L30 三角形の相似条件 の解答 :次>



数学名师 初中数学三角形相似问题这样解答就对了 冲刺数学满分



数学名师 初中数学三角形相似问题这样解答就对了 冲刺数学满分
相似比と面積比についての練習です。かなり基本的な話です。 苦手な人向けです。 次回追加分は面積について計算していくものになります。 17年9月12日 画像にあるような三角形の相似に関しての長さを求める問題です。三角形の相似条件 3組の辺の比 がそれぞれ等しい 2組の辺の比 と その間の角 がそれぞれ等しい 2組の角 がそれぞれ等しい 合同条件と似ているのがわかるかと思います。 1番目と2番目は「辺」が「辺の比」になり、3番目は「辺の長さに関する条件」がなくなったものです。 ではこの三角形の相似条件をどのように使うのか、実際に問題を解きながら見ていきどの三角形の合同を証明すべきか(17年度北海道) このブログは「図がシンプルだけど結構キツイ問題」を紹介する目的で最初は作りました。 だんだん色々な問題を紹介するようになりましたが。 今回は,初心に戻って,非常に図がシンプルだけど,何




7 相似三角形的性质 北师大版九年级数学上册电子课本 易学啦



4 4相似三角形的性质极其应用一 Ppt 沃文网wodocx Com
学習1 直角三角形・図形の折り返しと相似 問題 右の図のような,∠a=90° の直角三角形 abc があり, 頂点 a から辺 bc に垂線 ad をひく。 ⑴ 線分 cd の長さを求めよ。 ⑵ 線分 ad の長さを求めよ。 解 ⑴ abc ∽ dac だから ,ca :cd=bc acより 4:cd=5:4,cd=32 cm相似な図形のかき方、三角形の相似条件や、相似を利用した距離や高さの求め方を練習していきます。 プリント6枚 中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード・印刷(1) 例えば,3 辺が3cm,3cm,1cm の二等辺三角形と,3 辺が3cm,3cm,2cm の二等辺 三角形は相似ではない。 (2)(5) 2つの正三角形は同じ形になるので相似である。一般に正多角形(正三角形,正方形, 正五角形,正六角形・・・)の場合は相似になる。



冲击18年中考数学5 相似三角形综合问题




中考數學 相似三角形搞不懂這幾點 問題可就大了 Itw01
こんにちは。tanukiです。 三角形が相似になる条件は3つありますね。 1、2つの角がそれぞれ等しい 2、対応する2つの辺の比とその間の角がそれぞれ等しい 3、すべての辺の比がそれぞれ等しい 小学生の算数では9割以上(体感)が1の角がすべて等しいを使って解くことができるので、まず三角形abcと三角形def は相似。 08:36=1:de。 de=45m。 三角形abcと三角形dgh は相似。 08:28=1:dg。 dg=35m。 木の高さは3506=41m。 三角形abcと三角形def は相似。 08:24=1:de。 de=3m。 木の高さは305=25m。逆に,2つの三角形が相似であるとき,次の (1) (2) (3)はすべて成り立つ. 要点 (1) 2組の角がそれぞれ等しい (2) 3組の辺の比がそれぞれ等しい (3) 2組の辺の比とその間の角がそれぞれ等しい (解説) (1) 三角形の内角の和は180°だから「2組の角がそれぞれ等しい」とき,「3組の角がそれぞれ等しくなる」 相似であることを証明するには「2組」を示せば十分だと




九级数上册相似三角形的性质相似三角形中的开放性问题素材 新版 青岛版下载 Word模板 爱问共享资料



初二数学题 关于相似三角形 全等三角形的问题 数学作业 解题作业帮
d で,三角形の内角の和は180°なので, ∠bdc= 180 ° −2 a = 180 3 a = °− × 36° =180°− 108° = 72° (2) (1) で計算した角度を図に入れると,次のようになる。 2 角が等しいので, bcd はbc=bd の二等辺三角形, dab はda=db の二等辺三角 形になる。 三角形の相似条件と基本的な証明 三角形の相似条件と三角形の相似条件を使った証明問題です。 相似条件を使って相似な三角形を見つけるのは、応用問題や入試問題でよく出題されるので、しっかり出来るようにしてください。 三角形の相似条件は2年生で習った三角形の合数学35章図形と相似「相似な図形」<準備問題①> 組 番 名前 1三角形の合同条件を書きなさい。 2次の図で,AB//CDのとき,次の問いに答えなさい。 A B C D a 45° 110° a 50° 85° A C D B a ° 80° 130° A C D B a 25° 150° 75° A C D B



19年中考专题复习 相似三角形的存在性问题 三角形 定理 代数 新浪新闻



两边成比例 且夹角相等的两三角形相似 Page16 青岛版九年级数学上册电子课本 教材 教科书 好多电子课本网
図形の問題の組み合わせ。 相似比と面積比。 理解して押さえていないと苦しいと思うんだけどな。 まずは解答。 一行目に「⊿ADP∽⊿EBPだから」とあるけれど、まず解答でこの三角形の相似に着目したことがすんなりと理解できるだろうか? 説明できるC問題1(1) 相似形を利用して、図のxの長さを求めなさい。 基本的な解き方 2つの三角形が相似の関係ですから、 向きをそろえて2つの三角形を書き 、計算をします。 工夫をした解き方とスーパーテクニック 相似の計算問題 計算問題①「三角形の相似比を求める」 計算問題②「三角形の面積比を求める」 計算問題③「台形の中の三角形と面積比」 相似の証明問題 証明問題①「相似な三角形のペアを見つける」 証明問題②「三角形の相似を示す」




初三数学相似三角形




中考数学 三角形证明 题型总结 4
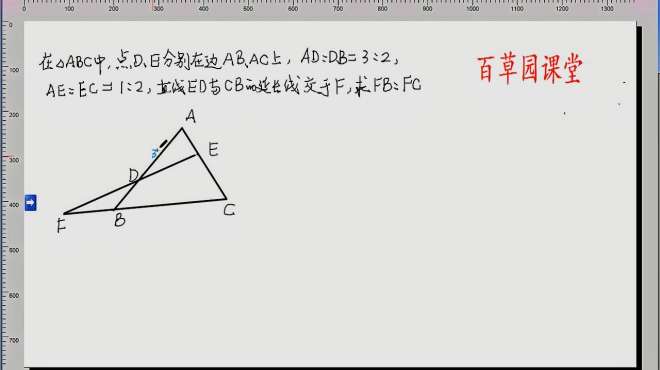
相似比の練習問題(三角形他2) 問1.次の各問いに答えなさい。 ab =8cm,bc =10cm,ca =6cm です。このとき、ec,ad の長さを求めなさい。 (イ)三角形abc で,辺bc 上に点d,辺ac 上に点f をとり,ad とbf との交点をe とする。三角形の相似 相似な図形 問題1 正解1 解説1 問題2 正解2 解説2 三角形の相似条件 問題3 正解3 解説3 問題4 正解4 解説4 相似の証明:2辺の比とその間の角 問題5 正解5 解説5 ----- 相似の証明:2組の角が等しい 三角形の相似条件と基本的な証明 三角形の相似条件と三角形の相似条件を使った証明問題です。 相似条件を使って相似な三角形を見つけるのは、応用問題や入試問題でよく出題されるので、しっかり出来るようにしてください。 三角形の相似条件は2年生で習った三角形の合同条件と似ていますが、相似は図形を拡大、縮小したものなので、辺の比が等しいことと



1



利用平行线构造相似三角形 用这道题来训练效果最好 知乎




中考真題詳解 因動點產生的相似三角形問題1 雪花新闻



中考数学相似三角形经典练习15题 吃透15题 相似没问题 中考 学习资料大全 免费学习资源下载




相似三角形性质的趣味故事 相似三角形的性质 三人行教育网 Www 3rxing Org



中考 因动点产生的三角形相似问题



图形变化中一脉相承的全等与相似问题 6 3相似图形 初中苏科版13版 数学中国网 Mathschina Com



相似三角形中的辅助线 学生版 教师版 沃文网wodocx Com



4 7 第2课时相似三角形 的周长和面积之比 免费资源共享课件巴巴www Kejian Com公众号kejianbaba打包 Ppt 课件巴巴kejian Com 课件巴巴kejian Com



二次函数与相似三角形的综合问题 动态问题要以静制动 动中求静




初三数学相似三角形综合题检测 有点难度 值得一练 网易订阅




全国初中数学竞赛辅导第三十六讲 相似三角形 一 北师大版下载 Word模板 爱问共享资料



相似三角形問題 初中數學常用解題方法 雪花新闻




中考数学 三角形证明 题型总结



利用几何变换解一类平几最值问题 翰林国际教育




一线三等角相似模型应用 参考网



期中考试压轴题大放送 相似三角形中的动点问题 初中年级 家长帮



數學名師 初中數學三角形相似問題這樣解答就對了 衝刺數學滿分 Zi 字媒體



百草园课堂 好看视频
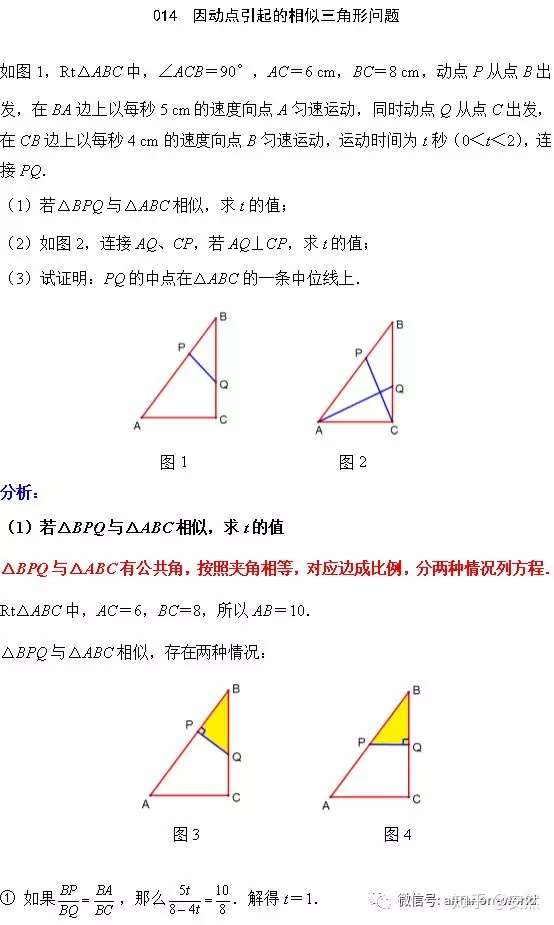



每日一题 初中 因动点引起的相似三角形问题 知乎




對應角單元二 Vnfp



相似三角形综合题 含中点问题 整理了多种方法 计算量很大 初中数学 学习资料大全 免费学习资源下载



数学之美 43 由勾股定理与相似进入玄幻的图形转换世界 简书
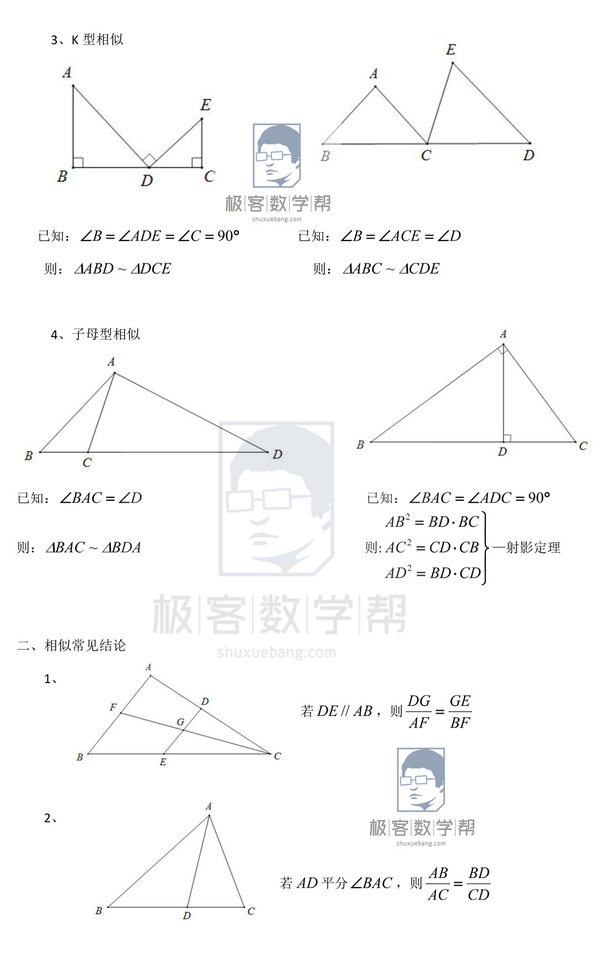



相似三角形搞不懂这几点 问题可就大了 教育频道 手机搜狐
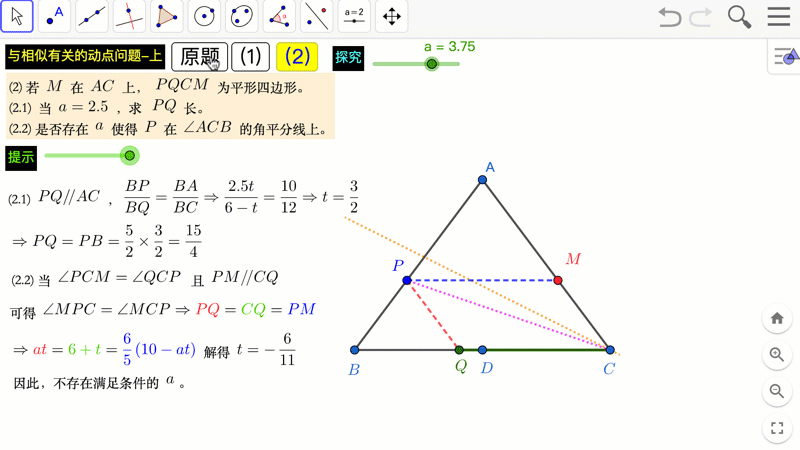



洋葱 与相似有关的动点问题 上 0051 Geogebra



用相似三角形解决问题 禾教 初中数学互动课堂



初一数学题相似三角形 信息图文欣赏 信息村 K0w0m Com



悟空问答 初中的相似三角形 中考怎么考 有什么好的解题技巧 小智教育的回答 0赞



相似三角形的应用 腾讯视频
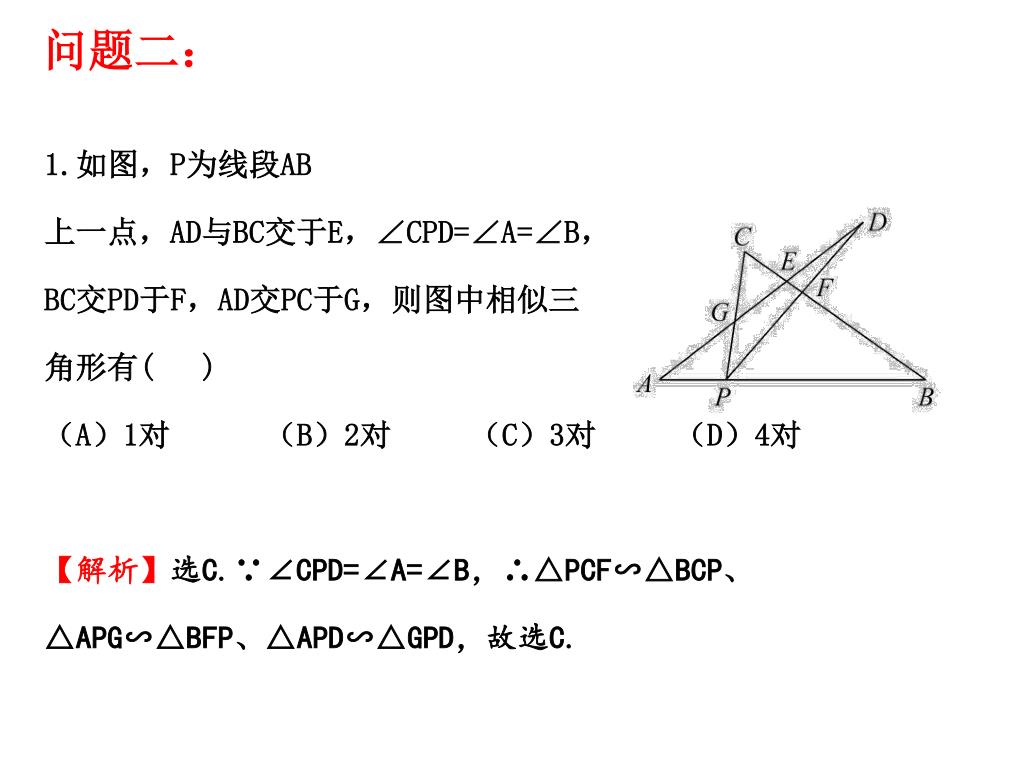



Ppt 中考第一轮复习 三角形相似powerpoint Presentation Id
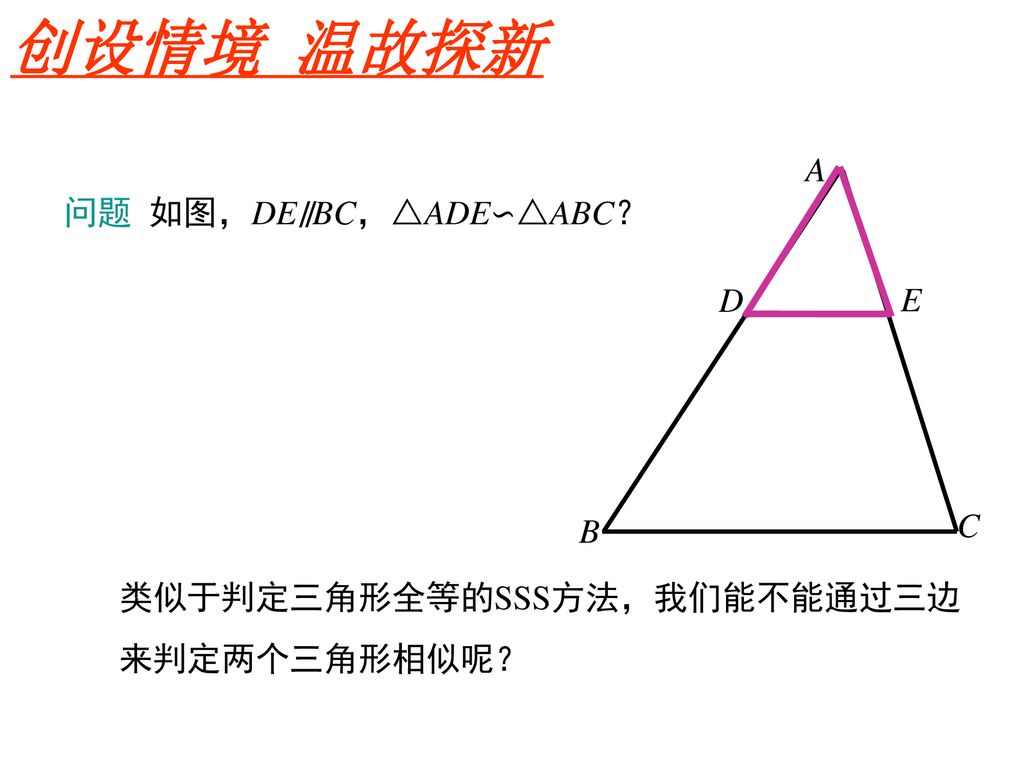



第二十七章相似相似三角形的判定第2课时三边成比例的两个三角形相似 Ppt Download
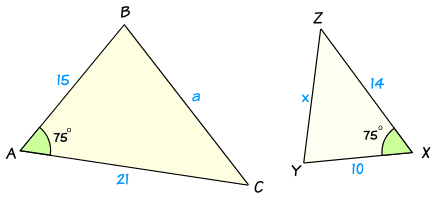



相似三角形的判定



今年数学难度不大 数学老师提醒 学生务必要重视这些题型 腾讯网
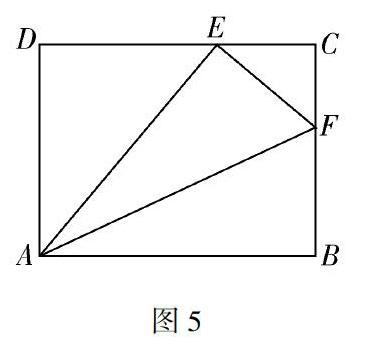



有数学味的 折纸中的相似问题 再探讨 参考网




幾何中的壓軸題熱點 掌握好相似類動點綜合問題 壹讀
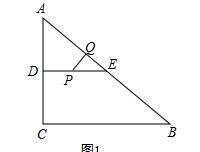



等腰三角形的存在性問題 與相似三角形相結合 綜合性強 楠木軒




ぜいたく中3 数学相似 子供のための最高のぬりえ



数学 相似三角形系列03 面积比问题



活用相似三角形中的对应高 科学猫



相似三角形的问题 图片欣赏中心 急不急图文 Jpjww Com




6 7用相似三角形解决问题学习与评价答案 苏科版九年级 初三 数学学习与评价答案 上下册 05网零5网0五网新知语文网



全等 相似 手拉手 闯江湖 育儿资讯 历史故事网



相似三角形的性质 图形的相似ppt 第2课时 第一ppt
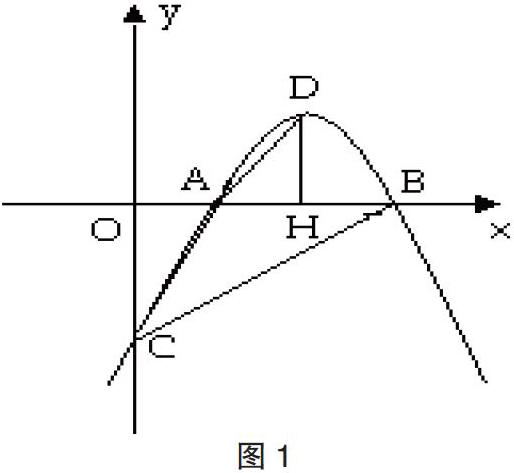



二次函数与相似三角形结合问题的教学探索 Www 366 Net Www366 Net必赢亚洲



2月17日9年级数学 相似三角形存在性问题 徐翔翔 1 哔哩哔哩 つロ干杯 Bilibili




19年1月4日陕西初中数学教师资格证面试真题 初中数学 相似三角形的应用 湖南教师招聘信息网



打印预览



呼和浩特 相似三角形開放和幾何動態問題應用方法 雪花新闻




常见三角形相似图形 相似三角形基本图形有哪些 三人行教育网 Www 3rxing Org



一线三等角模型 万图壁纸网
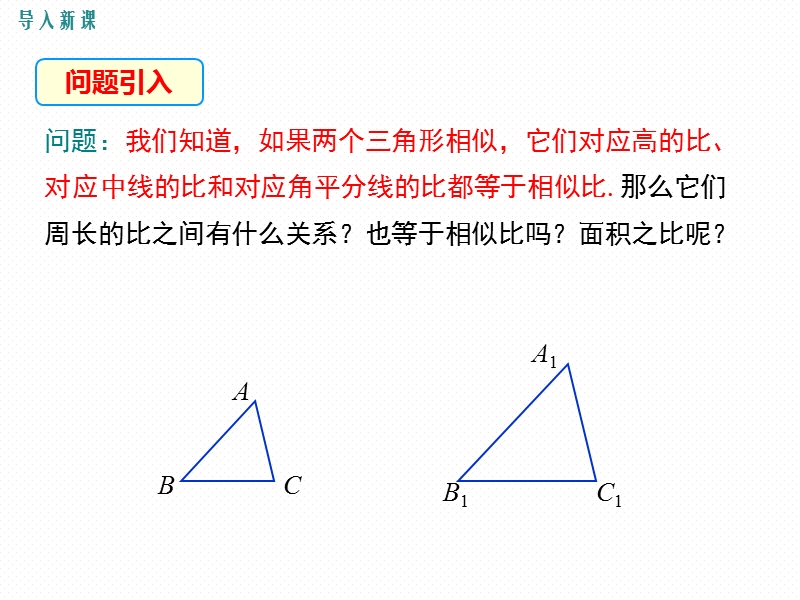



4 7相似三角形的周长和面积之比 第2课时 课件 七七文库www 77wenku Com



常见的相似三角形模型 柳树清风的学习笔记 微信公众号文章阅读 Wemp



数学 相似三角形系列03 面积比问题
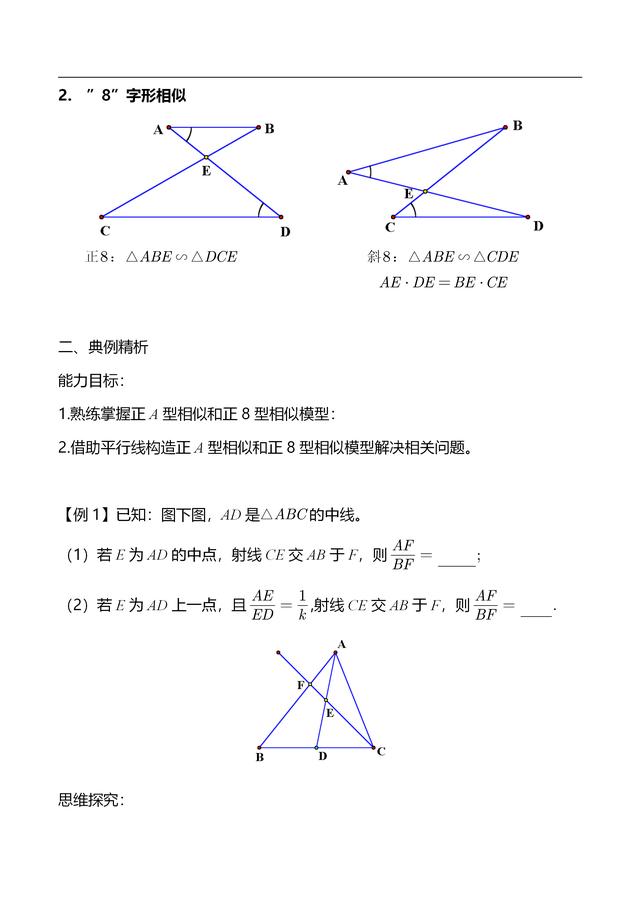



模型 相似三角形模型解析及辅助线作法梳理



探讨线段数量关系的解题策略 杂志论文 理科考试研究
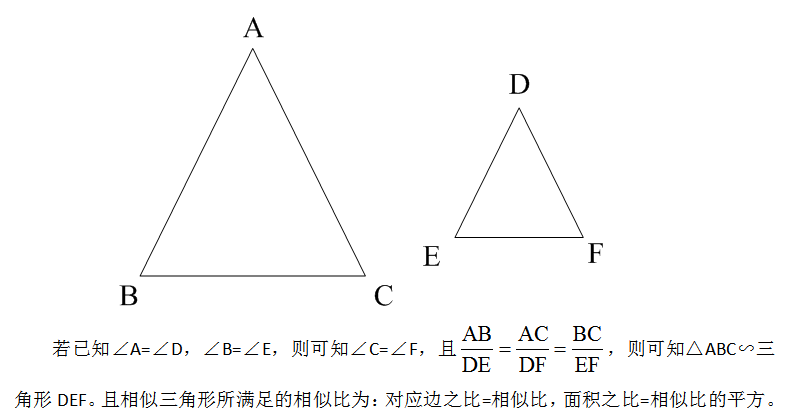



省考公务员 行测几何问题之相似三角形 知乎



相似三角形的性质 图形的相似ppt 第2课时 第一ppt



用几何变换再解衡水金卷三角形面积最大值问题 翰林国际教育



线段乘积问题必然与相似三角形有关 遇到了数学



中考数学倒计时18 二次函数的性质和三角形相似问题 中学解题思维 微信公众号文章阅读 Wemp



用相似三角形对应高的比等于相似比解决实际问题 哔哩哔哩 つロ干杯 Bilibili



课程信息 本讲教育信息 一 教学内容 相似三角形和三角形相似的条件 1 了解相似三角形 相似比的含义 2 掌握两个三角形相似 的判断条件 并能够运用三角形相似的判断方法解决一些简单的问题 二 知识要点 1 相似三角形 1 相似三角形 对应角




周长 面积 比 在平面几何问题中的巧用 每日头条




27 2 2相似三角形应用举例第2课时 Ppt 云豆网



27 2 3 相似三角形应用举例 人教版九年级下册数学电子课本 数九网



初三数学相似三角形的动点问题 信息阅读欣赏 信息村 K0w0m Com



中考 因动点产生的三角形相似问题



27 2 相似三角形 人教版九年级下册数学电子课本 数九网



初中数学 相似三角形 全等三角形 腾讯新闻




初中数学相似三角形的判定定理证明及利用三角形相似解决问题 每日头条



怎么证明两个三角形相似




九年级数学上册22 2相似三角形的判定第4课时相似三角形的判定定理3教案 沪科版 莲山课件




相似三角形对应边比例 相似三角形对应边成比例 这个是怎么证出来的 三人行教育网 Www 3rxing Org



相似三角形例题分析及知识点总结3600字 范文118




相似三角形



利用相似三角形解决圆中的线段问题 5 平行线型相似三角形例1 哔哩哔哩 つロ干杯 Bilibili



数学 相似三角形系列03 面积比问题




几何问题之相似三角形 网易订阅



看看下面的数学问题相似三角形的求高手 图片欣赏中心 急不急图文 Jpjww Com



解读相似三角形经典图形 科学猫




相似三角形模型讲解 一线三等角问题word版下载 Word模板 爱问共享资料



相似三角形搞不懂这几点 问题可就大了 教育频道 手机搜狐




得比换比 证相似 参考网



省考公务员 行测几何问题之相似三角形 知乎



初中数学相似三角形知识点汇总 秦学教育


